报名编号:CICC4035
团队名称:守序善良队
大家好,本篇是我们队伍的第六篇分享,主要内容是对于试商法除法器的简单介绍。水平有限,如有错误,欢迎大家批评指正。
设被除数dividend为A,除数divisior为B,位宽分别为M、N。二进制除法实际上和十进制的除法计算过程一样,下图是100110除110的例子。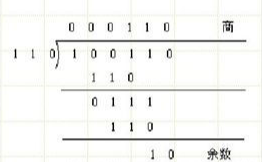
这种算法本质上是从被除数的第一位开始,截取宽度N的部分Q,例子中计算第一位是Q=100。判断Q是否比除数B的某一倍数大,取最大的倍数作为当前位的商。二进制除法即是判断Q是否比B大,如果比B大,那么商这一位是1,并取Q-B的结果作为下一次判定的Q。如果Q小于B,那么这一位商结果是0,同时Q按顺序再取一位,得到N+1宽度的Q,再次进行判定。依据这个算法,我们很容易写出一个基本的除法器。但是这种算法要求我们知道除数B的实际位数,即不为0的最高位是多少。显然现实生活中我们只知道输入B是一个32位、8位的数,无法直接判断不为0的最高位。当然,也可以通过前置的电路首先进行判断,再将结果作为输入给到这种除法器。
下面我们介绍一种不需要前置计算的除法器,试商法除法器。
试商法除法器实际上就是在基本除法原理的基础上稍加改动。在基础除法原理种我们不难发现,对实际商结果有影响的并不是Q的位数,而是Q是否大于B。因此试商法就是从A的最高位开始,Q=A[n-1],如果Q>B,和上一节方法相同。如果Q
试商法除法器不需要进行前置计算,对于基本除法器有一定的性能提升,但是仍然需要大于被除数位宽的时钟周期才能完成数据计算,因此对于E203的除法器性能提升并不显著,在提升E203的MDV模块性能时可借鉴参考试商法原理,寻求提升更为显著的除法器算法。
本文参考:
https://blog.csdn.net/blueteeth_/article/details/128888764