队伍名称:东莞庄路三缺二 队伍编号:CICC1399。大家好,本篇是我们队伍的第三篇分享,主要介绍加速RSA算法加速的思路。水平有限,如有错误,欢迎大家批评指正。
1 关于RSA算法
RSA为非对称加密算法(也称为公开密钥算法),是当前比较普遍使用的非对称加密算法之一,常用于密钥交换和数字签名。RSA是一种较为高级、可基于硬件和软件实现的加密算法,安全性能高,速度却由于计算量大而比较慢。算法基于数论原理,寻求两个大质数并将它们的乘积作为公钥(乘积进行因式分解极其困难),RSA算法的密钥和输入内容没有固定长度,一般1024 bits,密钥长度越长保密强度越高;模式为加密和解密,是两种RSA的工作方式。
RSA算法流程:
①
选取两个质数q和p,两个数相乘得到N。质数越大保密程度越高。
②
计算q-1和p-1的最小公倍数L。选取加密用的指数幂E为比1大且比L小,同时E和L的最大公约数为1。
③
选取解密时用到的指数幂D为E关于模数L的模逆元,即D=E-1(mod L);1
④
设明文为M,密文为C.。
则加密过程为:C=ME mod N;其中(E , N)组成公钥。
解密过程为:M = CDmod N;其中(D , N)组成私钥。
2 关于加速操作
上述提到N、E、D一旦选取,在给数据流进行加解密的过程中便是作为常数存在,不需要反复生成,在数据流达到一定长度的情况下,生成公钥和私钥的花费的时间占比很小,不考虑对它们进行加速。而实际应用中这3个常数数值往往很大,对应二进制数位宽一般为1024bits,甚至更多。这就会造成加解密用到的大数模幂运算花费的时间会很大,它也是我们要关注的加速操作。
对大数模幂操作常用的方案是【L-R扫描模幂算法+蒙哥马利模乘算法】。
L-R扫描模幂算法:
输入: M ,e,N,R2N;
-- M是明文,位宽取n=1024bits。
-- e 是加密密钥,位宽取 n。
-- N 是模数,位宽取n。
-- R2N是常数, 等于R2modN,用于抵消蒙哥马利模乘结果的冗余项。
输出:C=MemodN;
{
M2
= Monprod(M,R2N,N)
C =Monprod(1,R2N,N)
for
i = n-1 to 0 do
{
C
= Monprod(C,C,N) ;
if(ei
= 1) C = Monprod(C,M2,N);
}
C=Monprod(1,C,N)
reture
C;
}
蒙哥马利模乘算法:
输入
: A,B,N;
--A = [am+2,am+1,am,am-1,am-2,…,a1,a0
]2,
--B = [bm+2,bm+1,bm,bm-1,bm-2,…,b1,b0]2,
--N = [nm-1,nm-2,…,n1,n0]2,n0=1。
--A
输出: S= Monprod (A,B,N) = A * B * 2-(m+3) mod N;
S = 0;
for(i= 0;i< m+3 ; i++){
if(ai == 1) then S = S + B;
if (S[0] ==1)then S = (S+N)/2; }
这里要注意的是多循环三次(m+3)是为了省去算法每次循环原有的操作(if(S>N)S=S-N;),进一步减少运算时间。
可以看出L-R模幂算法包含了大量蒙哥马利算法实现的模乘运算。模幂运算效率的提高取决于模乘运输速度。为了加快模幂运算速度,我们将模乘运算操作交给硬件完成,而for loop等数据调用工作交给软件实现。
3 关于硬件实现与仿真
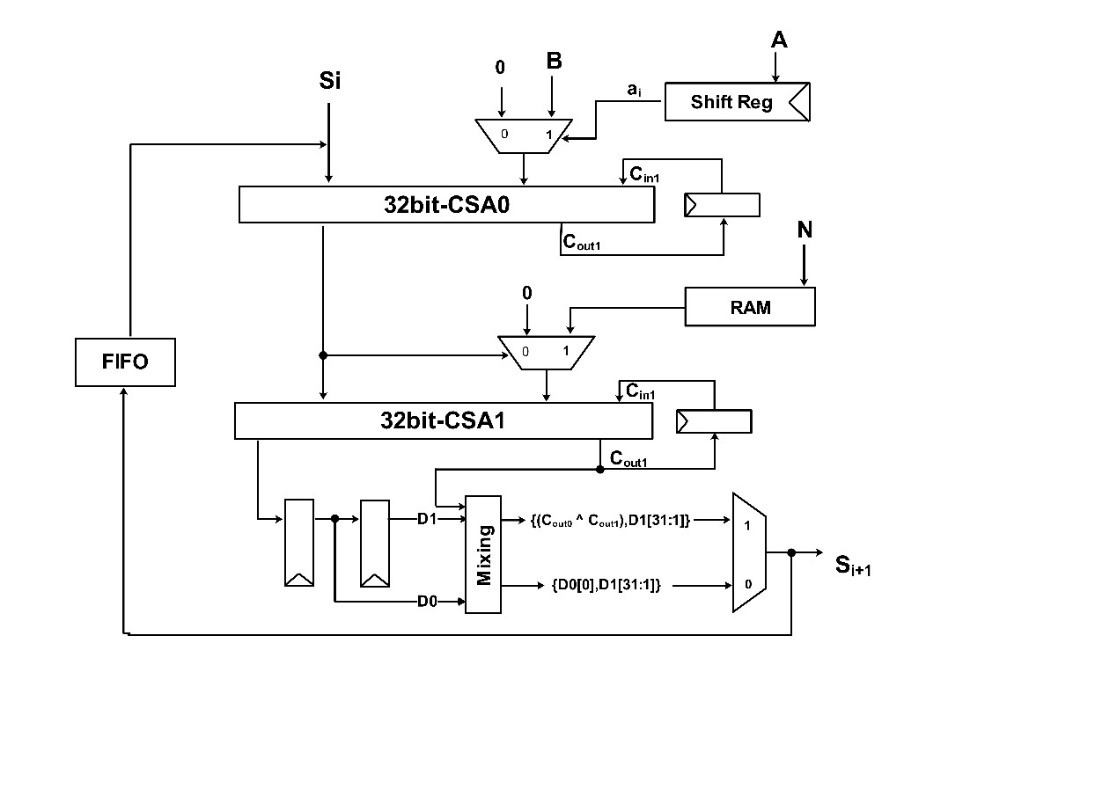
图1蒙哥马利模乘电路结构
图1所示电路可以实现1024bits模乘运算,主要特征包括:
① 使用32位加法器完成1024bit加法运算,节省硬件开销。
②
使用同步FIFO存取模乘结果S,无需外部读写地址线实现字段更新与读取操作同时进行。
③ 使用双DFF结构实现各字段右移一位,当前字段最高位补下一个字段的最低位。
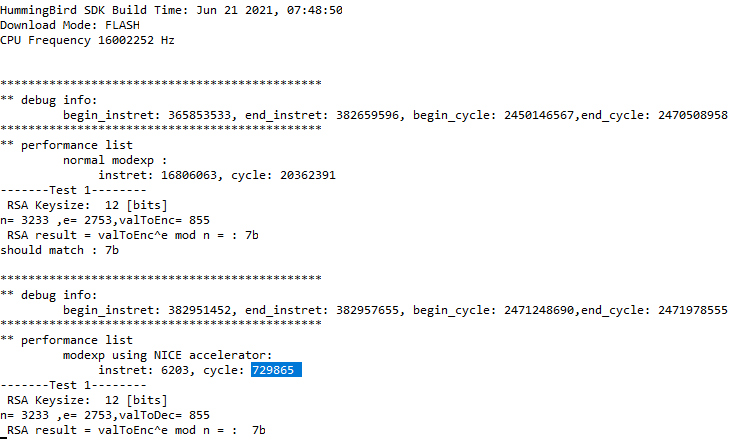
图2 RSA算法加速结果
最后给出RSA算法的加速结果,如图2所示,时钟周期数加速了27.9倍。