CNN即卷积神经网络(Convolutional Neural Networks),是一类包含卷积计算的神经网络,是深度学习(deep learning)的代表算法之一,在图像识别、语音识别等场景取得巨大的成功。
CNN的发展史:
提到CNN的发展史,就要提到多层感知器(Multi-Layer Perception, MLP)。(图片来源于3Blue1Brown)
MLP其实是对神经元的模拟和简化。
单层感知器(Single Layer Perceptron):
单层感知器用来模拟单个神经元。

左图是神经元,右图是抽象出的数学模型。
树突:用来接收别的神经元传递的信息,对应数学模型的输入,多个输入有不同的权重
细胞核:用来处理所接收的信息,对应数学模型的sum求和+激活函数f,意味着:当信号大于一定阈值时,神经元处于激活状态。
轴突:用来将信息传递给其它神经元。对应数学模型的输出。
多层感知器(MLP):
单层的感知器只能解决一些简单的线性问题,面对复杂的非线性问题束手无策,考虑到输入信号需要经过多个神经元处理后,最后得到输出,所以发展出来了多层感知器,引入了多个隐藏层,如下图所示:
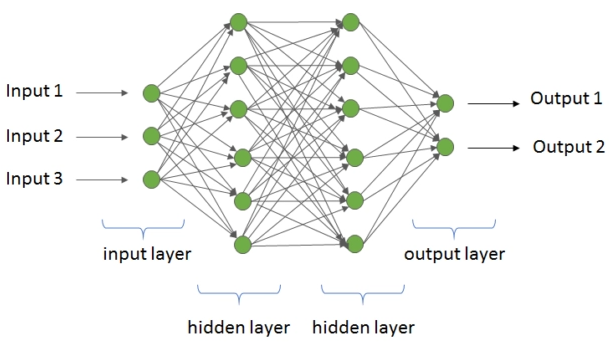
所以多层感知器 = 全连接层 + 激活层,多层感知器可以逼近任意函数。但是多层感知器有两个显著缺点:
1. 多层感知器没有考虑到图像的空间结构,识别性能受到限制。(比如数字识别,将数字平移到图像另一个位置,被认为是不同的图片)
2. 参数量太大,难以训练,容易陷入局部极值,
这样便有了后来的CNN,CNN是减少模型尺寸的利器。
CNN常见的层包括:全连接层、卷积层、池化层、激活层等。
多层感知器包含全连接层和激活层,CNN在多层感知器的基础上加入了卷积层(池化层其实也是卷积运算,用来减少数据规模的)
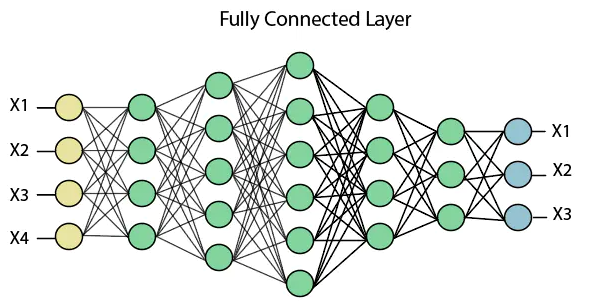
全连接层(Fully connected dence layers),正如其名,指的是层中的每个节点都会连接它下一层的所有节点。理论上讲,只要神经元足够多(图中绿色圈),神经网络可以逼近任意函数。
全连接层输出尺寸的计算公式:
全连接的实质就是矩阵相乘,如下图所示:输入向量X乘以权重矩阵W,加上偏置B得到输出,所以输出向量大小等于权重矩阵的行数。
# 计算公式
Y = WX + B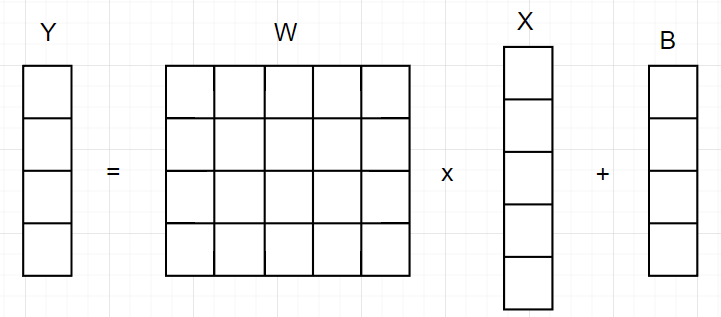
对于一张输入图片,大小为[W, H],如果生成一张[X, Y]的特征图,需要WHXY个参数,这即是全连接层(Fully connected dence layers),这个参数量实在太庞大,网络很难训练。
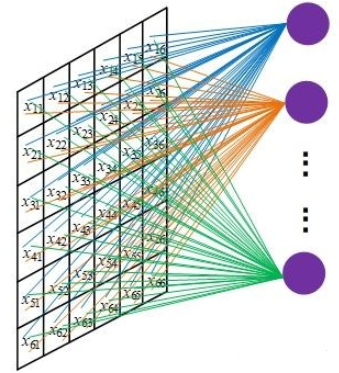
卷积层的本质就是用来解决这种计算量爆炸的问题。
卷积的核心思想是:
局部感知域
权值共享
局部感知:
局部感知的一层的神经元只连接到前一层的局部区域,不同于全连接。这样做也有神经学原理支撑:一个神经元并非接收其它所有神经元传来的刺激都产生反应,它首先会将其相邻神经元传来的刺激进行积累,到一定时候产生自己的刺激并传递给一些与它相邻的神经元。这个相邻就是局部感知的概念,对于图像识别而言,其的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱。因此,每个神经元其实没有必要对全局图像进行感知(全局连接),只需对局部进行感知(局部连接),然后在更高层将局部信息综合起来就得到了全局信息。
下图展示了全连接与局部连接的差别:
全连接的参数可以从10^12次降到10^8
权值共享:
采用局部连接后,参数还是太多了,需要引入权值共享的概念,如上图的局部连接中,对于1M个神经元,每个神经元的感知野为10x10,那么参数量即为 1M * 10 * 10,如果这1M个神经元的10 * 10的参数都是相等的,那么参数量将会降为100了。
其中隐含的原理是:图像的一部分统计特性与其它部分是一样的,意味着:对于图像的所有位置,可以使用相同的权重值。
卷积层的计算过程:
如下图(来源于网络,侵删)所示展示了:
输入(1, 5, 5, 3),意思是batch=1,图像HeightIn = 5, WidthIn = 5, channel = 3(代表RGB三颜色通道)
卷积核:(2, 3, 3, 3),意思是2个卷积核,图像HeightKernel = 3, WidthKernel= 3, channel = 3(与输入channel必须相等)
填充:padding = 1
步长: stride = 2
输出:(2, 3, 3),表示2个feature map,提取2类特征。
卷积层输出尺寸的计算公式:
HeightOut = (HeightIn - HeightKernel + 2 * padding) / stride + 1
Widthout = (WidthIn - WidthKernel + 2 * padding) / stride + 1池化即下采样(downsamples),一般在卷积层后面,目的是为了减少特征图(减少网络的参数),从而减小计算量,并且在一定程度上能控制过拟合。
常见的池化层为最大值池化层(max-pooling)与平均值池化层(mean-polling),
如下图所示,其stride为2,保证两个池化区不重叠(否则为重叠池化)
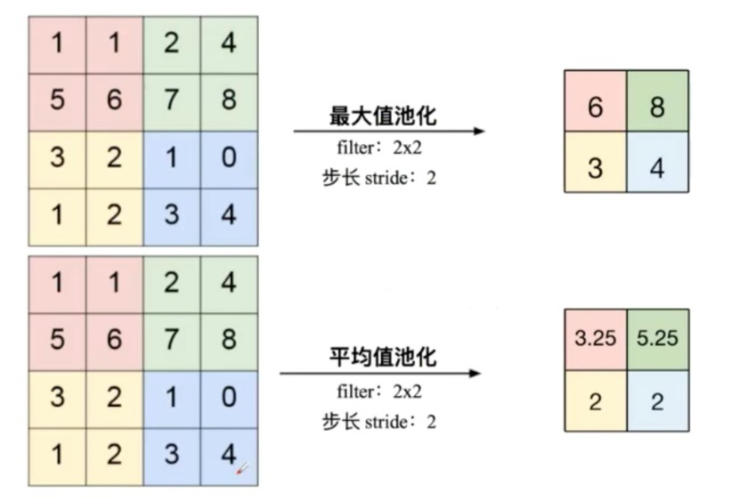
池化层输出尺寸的计算公式:
HeightOut = (HeightIn - HeightKernel + 2 * padding) / stride + 1
Widthout = (WidthIn - WidthKernel + 2 * padding) / stride + 1CNN中经常是一个卷积层后跟一个激活层,激活层是一个非线性层,正如神经元有一定的阈值,只有信号强度大于某个值,神经元才能被激活,将信号发射到下一个神经元。
其数学可视化过程如下图所示(图来源于网络):

为什么要引入激活层?
以下回答引用自参考6:
引入激活函数是为了增加神经网络的非线性,如果不用激活函数,每一层都是上一层的线性输入,这样一来,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机。引入激活函数则引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
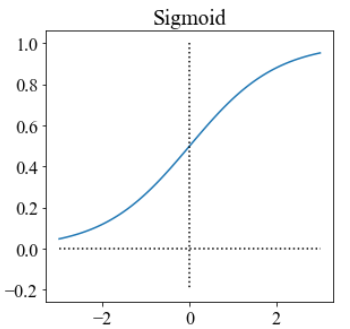
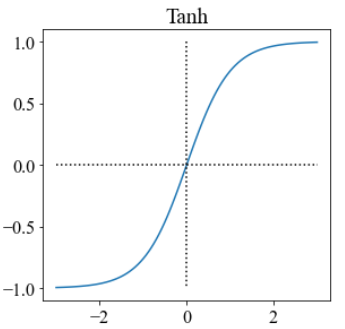
常见的激活函数有如下几种:
sigmoid
tanh
relu
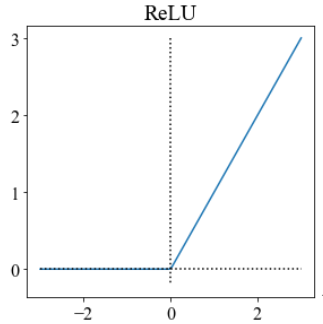
它们各自有其优缺点,现在常用的是relu,其不需要指数运算,复杂度低,且不会出现梯度饱和、消失问题,收敛速度快。
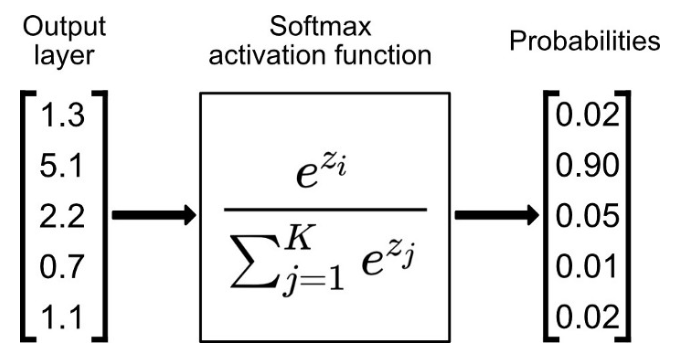
Softmax 是用于多类分类问题的激活函数,在多类分类问题中,超过两个类的标签则需要类成员关系。是sigmoid在多分类上的推广,目的是将多分类的结果以概率的形式展现出来,对于长度为 K 的任意实向量,Softmax 可以将其压缩为长度为 K,值在(0,1)范围内,并且向量中元素的总和为 1 的实向量。