报名编号：CICC1740 团队名称：小型三极管
主要的除法运算优化方法是使用基本的SRT-4算法进行除法运算，以模拟SRT-64除法运算:
为了减少时钟周期并提高运算频率，极大基法是SRT算法中提出的一种方法。在该方法中，每次迭代的位数取决于所使用的基数r，即r=2b（其中b为每次迭代获得的结果位数）。虽然基数为64时每次迭代可以得到6位，理论上只需11个周期即可完成，但商选过程十分复杂，查找表的面积随着r成2的指数幂增长，即使是最小冗余也会产生超大的面积，得不偿失。为了缩短运算周期，可以使用基数为4的数位递归SRT算法（每次迭代结果为2位），模拟基64的SRT算法，每个循环重复多次，每个周期进行3次迭代，即6位/周期，等效于基数为64的递归除法。与极大基64方法相比，该方法的硬件结构和面积大幅减少，运算的时钟周期也得以缩短。
为了实现优化，设计的硬件结构需要在一个周期内同时完成三次基数为4的迭代。为了增加基数为4的迭代次数，可以使用基数差分的方法。尽管相比基数为4的SRT算法，这种方法增加了硬件的面积，但与基数为SRT16的算法相比，硬件结构并没有太大变化。基数为4的SRT算法中的部分余数运算可以表示为Rj+1=4Rj-q_(j+1)d，这个过程需要进行三次。对于中间三次迭代中多组数据的相加，可以使用CSA加法器来提高运行速度。该结构如图所示，将中间步骤的Rj分为Sj和Cj两部分。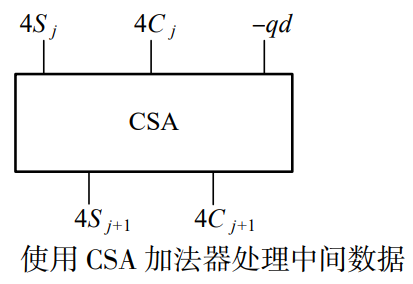

该结构是三输入二输出的，内部没有进位，可以看作没有任何时间上的冗余。整个CSA的延迟与一位全加器相同，不受数据位宽的影响，适合于对多组相加数据做中间值管理。此外，使用多个CSA器件还可以实现数据压缩的效果。在除法中，商数值的选择是最占用硬件面积的，因此设计适当的共用商数选择查找表逻辑非常关键。具体实现中，可以选择最大冗余度q∈(-3,-2,-1,0,1,2,3)d，也可以选择最小冗余度q∈(2,-1,0,1,2)d[10]。使用最小冗余度可以避免在运算过程中遇到(3d,-3d)的情况，其中2d和-2d可以通过对d和-d移位来产生。