队伍编号:CICC3280 团队名称:芯新星队
接上文对e203内部乘法运算部件结构算法的研究,我们继续进行了Wallance树和压缩器的研究
若要在单周期内处理内处理多个需要相加的数,Wallance树是一种非常常用的方法,与普通的加法器相比,它的组合更灵活,门电路的延迟更低。简单地讲即许多个加数求和,每3个加数分为一组,压缩至2个加数,循环往复。总之,是一种以资源换速度的体现。
Wallance树的主要组成是3:2压缩器(即CSA)和4:2压缩器。
3:2压缩器本质上就是一个全加器,如下图即为3:2压缩器的结构: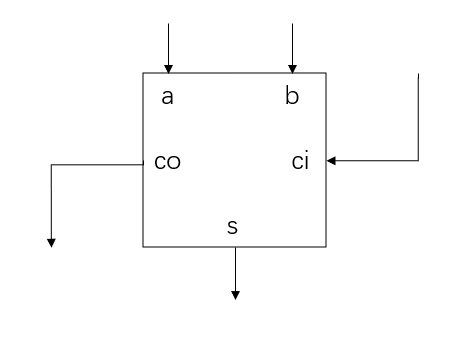
而4:2压缩器从作用上可以理解为两个CSA实现的,如下图所示: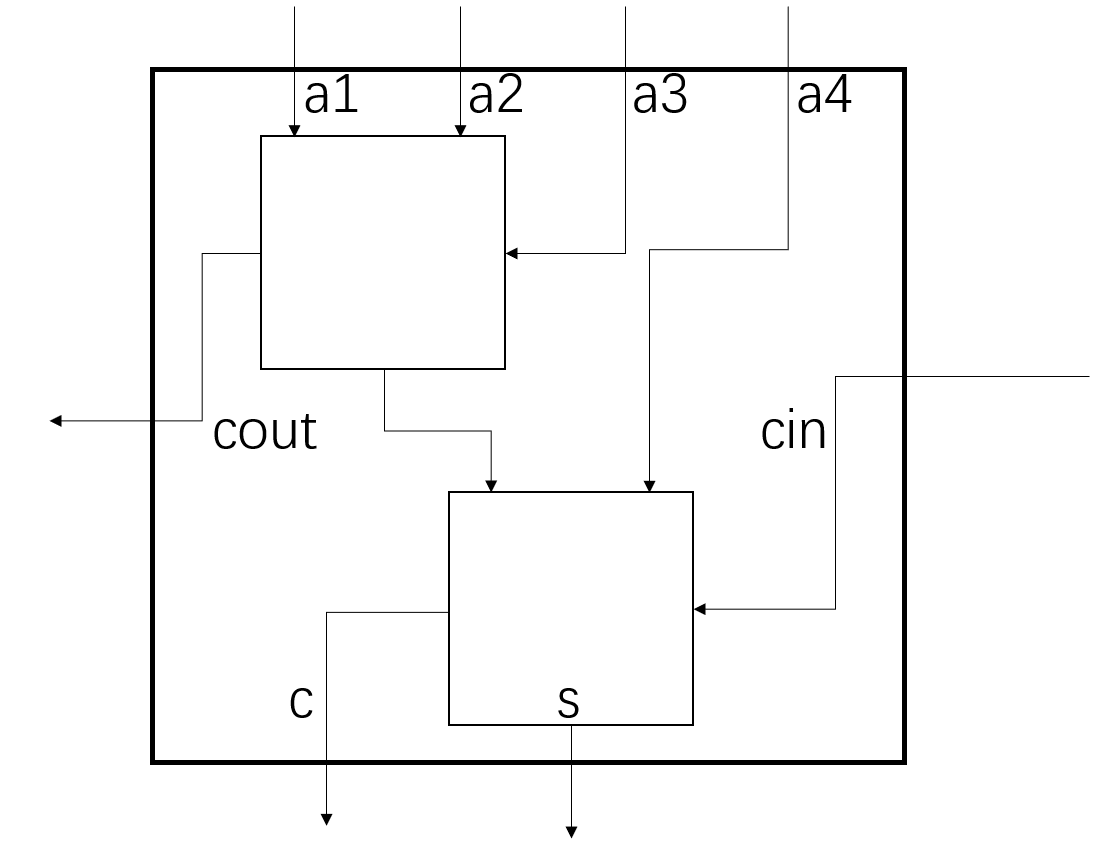
将4:2压缩器理解为两个3:2仅仅是为了便于理解,在原理上有更优的实现方法,如下图所示: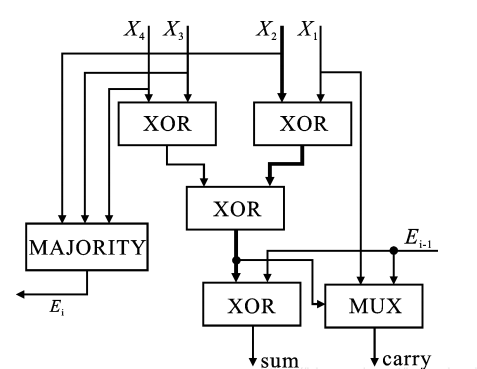
与第一种相比,改进型的4:2压缩器做到了更低的电路延迟,同时也可以实现并联,因此可以实现更好的性能。在工程中,3:2压缩器与4:2压缩器的实现如下:
module csa(input a,
input b,
input ci,
output s,
output co);
assign s = a ^ b ^ ci;
assign co = (a & b) | (a & ci) | (b & ci);
endmodule
module four2two(
input a1,
input a2,
input a3,
input a4,
input cin,
output s,
output c,
output cout);
wire a12 = a1^a2; wire a34 = a3^a4; wire a1234 = a12^a34;
assign s = cin^a1234;
assign cout = a34 ? a2 : a4;
assign c = a1234 ? cin : a1;
endmodule
将两种压缩器结合使用,即可将多个部分和较快速的相加。
Wallance的树性结构如下图所示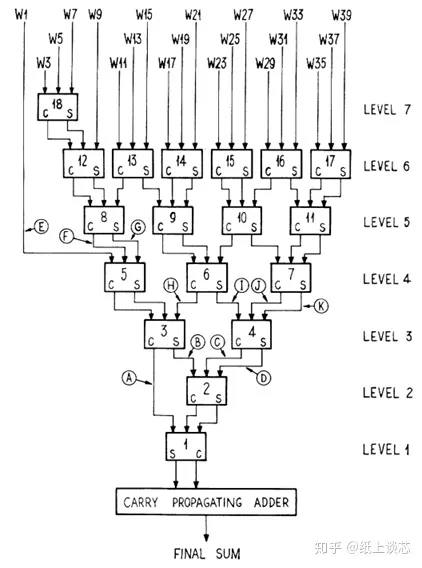
Wallance树的具体算法讲解可参照以下文章https://zhuanlan.zhihu.com/p/130968045