喜欢0次
1 队伍介绍
报名编号:CICC1981
团队名称:鼠队
团队成员:赵嗣纬,熊园园,林欣铨
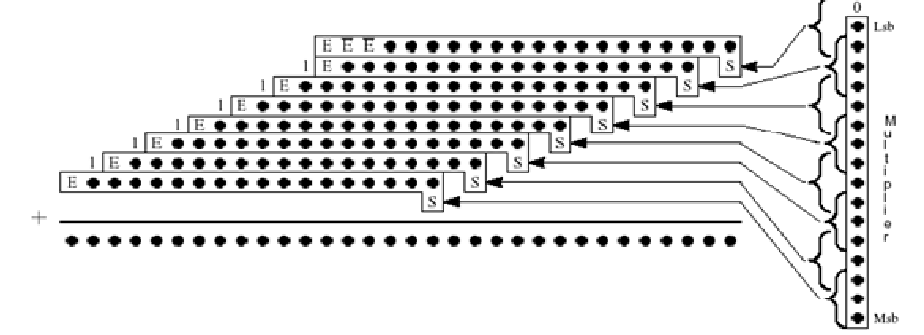
在 Booth乘法中,对部分积累加求和,必须对它们的高位部分进行符号位的扩展,保证每个部分积的最高位对齐,才能得到正确结果,如图所示。
在图中的点状积阵列中,扩展出的符号位占1/3。对这个阵列求和会导致较多的硬件资源浪费,也增加了计算的功耗,使用一种有限符号扩展技术,有效的解决了符号位过多的问题。
有限符号扩展技术描述如下:例如,把8bit有符号数SXXXXXXX扩展为12bit,其中S表示符号位,X表示数据位。采用符号位直接扩展时,可以得到SSSSSXXXXXXX。对其进行等价逻辑变换:
于是,符号位扩展转化成为:对原操作数的符号位取反,并在高位直接补0,再对第二项的确定部分进行补偿。采用有限符号扩展技术对部分积进行处理,点状积的个数从图中的256个减少到177个,而且“扩展符号位”E的生成逻辑非常简单。